| Systems of Equations |
|---|
|
Two or more equations put together are called Systems of Equations. |
Below, we have a system of equations:
2y = x + 1
3x = 4y - 1
The solution of a system of equations is called an ordered pair (x, y).
Below are examples of some of the linear and quadratic functions we've already learned about:
|
Figure 1. |
|---|
| Quadratic Systems |
|---|
|
Quadratic systems are sets of quadratic equations that have variables with the same values. For example: 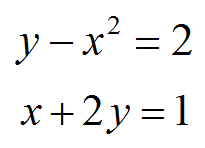
The solution of a system of equations is called an ordered pair (x, y). There may be multiple (or no) solutions. |
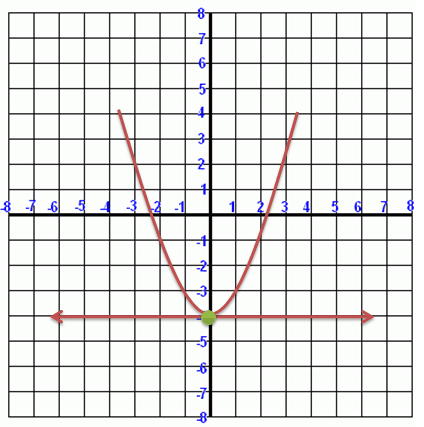
|
Figure 2. |
|---|
The above system has a solution at (0, -4).
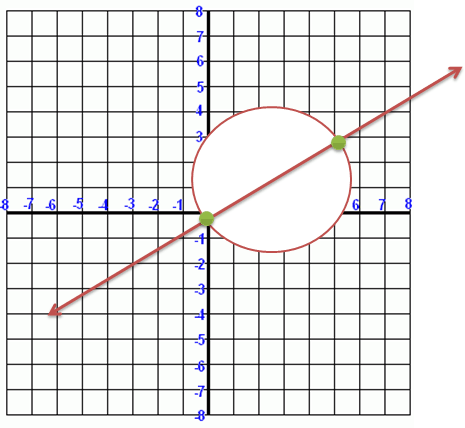
|
Figure 3. |
|---|
The above system has two solutions at roughly (0, -0.2) and (5, 2.8).
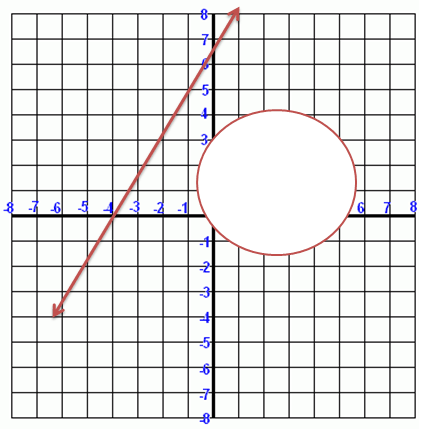
|
Figure 4. |
|---|
The above system has no solutions.
Let's solve the system of equations below:

|
Figure 5. |
|---|
To graph, first we must convert both equations to slope-intercept form:
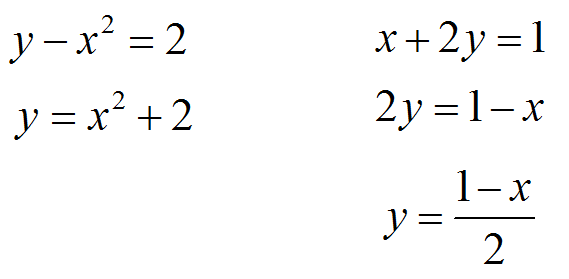
|
Figure 6. |
|---|
Now, we graph the equations:
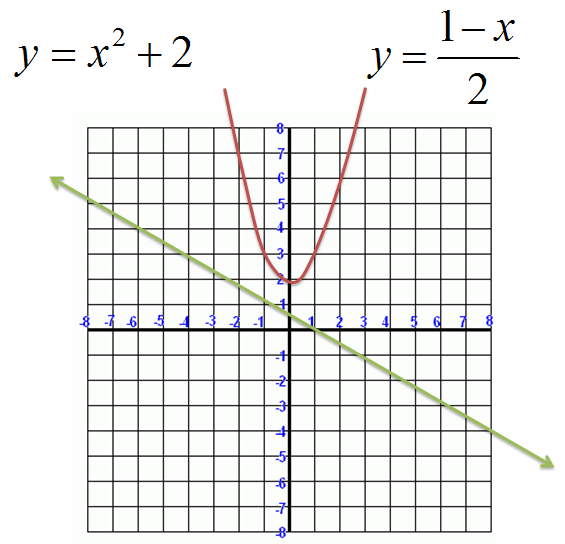
|
Figure 7. |
|---|
This system of equations has no solution.